Aritmetica

El maga principal aritmetico operacion son el adicion, el sustraccion, el multiplicacion y el division.

El aritmetica es un elemental rama del matematica que ta estudia con el maga numerical operacion como el adicion, el sustraccion, el multiplicacion y el division. Na un mas amplio acepcion, ta inclui tambien ele con el potenciacion, el extraccion de maga raiz y el toma de maga logaritmo. Distinguible el maga aritmetico sistema basao na el tipo de numero na el que ta opera ellos. Restringio el entero aritmetica lang al maga calculacion con el maga positivo y negativo natural numero. Ta involucra el aritmetica del maga racional numero con el maga operacion na el maga fraccion que ta yace entre el maga entero. Ta inclui el aritmerica del maga real numero con el calculacion, y con el maga racional y con el maga irracional numero, y ta cubri con el entero real recta. Otro distincion basao na el sistema de numeracion empleao para realiza con maga calculacion. El decimal aritmetica el mas comun. Ta usa ele con el maga basico numero de 0 a 9 y el de ellos maga combinacion para expresa con el maga numero. El binario aritmetico, por el contrario, usao por el mayoria del maga computadora y ta representa con el maga numero como maga combinacion del maga basico numero 0 y 1. Ta opera cuanto aritmetico sistema na maga matematico objeto hinde numerico, como el aritmetica de maga intervalo y el aritmetica de maga matriz.

Ta forma el maga aritmetico operacion con el base de manada rama del matematica, como el algebra, el calculo y el estadistica. Ta juga ellos con un similar papel na el maga ciencia, como el fisica y el economia. Presente el aritmetica na manada aspecto del cotidiano vida, por ejemplo, para calcula con el cambio durante un compra o para maneja con el maga personal finanza. Es uno del mas temprano forma del matematico educacion que ta incuntra el maga estudiante. Ta estudia el psicologia y el filosofia con el maga cognitivo y conceptual fundacion del aritmetica.

Ta remonta a maga mil, y seguro maga decena de maga mil, año el practica del aritmetica. Ya inventa maga antiguo civilizacion, como el egipto y el sumerio, con maga sistema de numeracion para soluciona con maga practico aritmetico problema tan temprano como 3000 AEC. Empezando na el aca-7 y aca-6 maga siglo AEC, ya inicia el maga antiguo griego con un mas abstracto estudio del maga numero y ya introduci con el metodo de maga rigoroso demostracion. Ya desarrolla el maga antiguo indio con el concepto de cero y el indo-arabigo numeracion, que ya refina mas el maga arabigo matematico y ya difundi al occidente durante el Medio Edad. Inventao el maga primero mecanico calculadora durante el aca-17 siglo. Ya mostra el maga aca-18 y aca-19 siglo con el desarrollo del moderno teoria de maga numero y el formulacion del maga axiomatico fundacion del aritmetica. Durante el aca-20 siglo, ya revoluciona el aparicion del maga electronico calculadora y el maga computadora con el precision y el velocidad con el que realizable el maga aritmetico calculo.

Definicion, etimologia y maga relacionao rama

Ta tene el termino "aritmetica" con el de suyo raiz na el latin termino "aritmetica", al de suyo vez derivao del maga antiguo griego palabra ἀριθμός (arithmos, "numero") y ἀριθμητική τέχνη (arithmetike tekhne, "el arte del cuenta").

Hay maga desacuerdo sobre el de suyo preciso definicion. De acuerdo con un estrecho caracterizacion, ta trata el aritmetica con el maga natural numero lang. Sin embargo, ta inclui el mas comun vista con el maga operacion sobre el maga entero, el maga racional numero, el maga real numero, y tiene vez sobre el maga complejo numero na el de suyo ambito. Ta restringi cuanto definicion del aritmetica al campo del maga numerico calculacion. Entendio na un mas amplio acepcion, ademas ta inclui ele con el estudio del desarrollo del concepto del maga numero, el analisis del maga propiedad y el maga relacion entre el maga numero, y el examen del axiomatico estructura del maga aritmetico operacion.

Intimamente relacionao el aritmetica con el teoria de maga numero y, para cuanto autor, sinonimo el dos maga termino. Sin embargo, na un mas especifico acepcion, restringio el teoria de maga numero al estudio del maga entero, y ta enfoca este na el de suyo maga propiedad y maga relacion, como el divisibilidad, el factorizacion y el primalidad. Tradicionalmente conocio este como superior aritmetica.

Tambien intimamente conectado el aritmetica a manada rama del matematica que ta depende de maga numerico operacion. Basao el algebra na maga aritmetico principio para resolve con maga ecuacion usando con maga variable. Tambien ta juga este maga principio con un importante papel na el calculo na el de suyo intento de determina con el maga tasa de cambio y el maga area bajo maga curva. Ta usa el geometria con maga aritmetico operacion para medi con el maga propiedad del maga forma mientras que ta utiliza el estadistica con ellos para analiza con maga numerico dato.

Maga numero

El maga numero son maga matematico objeto usao para conta con maga cantidad y medi con maga magnitud. Son maga fundamental elemento na el aritmetica ya que todo el maga aritmetico operacion realizao na maga numero. Hay maga diferente tipo de maga numero y diferente maga sistema de numeracion para representa con ellos.

Maga tipo

Diferente maga tipo de maga numero na un real recta. Negro el maga entero, azul el maga racional numero, y verde el maga irracional numero.

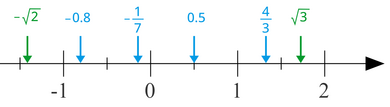
El maga principal tipo de maga numeros empleao na aritmetica son el maga natural numero, el maga entero numero, el maga racional numero y el maga real numero. El maga natural numeros son el maga entero numeros que ta comenza desde 1 y ta llega hasta el infinidad. Ta exclui ellos con 0 y el maga negativo numero,. Ademas conocio ellos como el maga numero de cuenta y expresable como {1, 2, 3, 4, ...}. El simbolo del maga natural numero es $\mathbb {N} .$ Identico el maga entero numero al natural numero con excepcion de que ta inclui ellos con 0. Expresable ellos como {0, 1, 2, 3, 4, ...} y ta tene ellos con el simbolo $\mathbb {N} _{0}$. Hinde ta distingui cuanto matematico con el distincion entre el maga entre natural numero y el maga entero incluyendo con el 0 na el conjunto del maga natural numero. Ta abarca el conjunto de maga entero numero tanto con el maga positivo como el maga negativo entero numero. Ta tene ele con el simbolo $\mathbb {Z}$ y expresable como {..., -2, -1, 0, 1, 2, ...}.

Racional un numero si representable como el razon entre dos maga entero. Por ejemplo, formao el racional numero ${\tfrac {1}{2}}$ dividiendo con el entero 1, llamao el numerador, por el entero 2, llamao el denominador. Otro maga ejemplo son ${\tfrac {3}{4}}$ y ${\tfrac {281}{3}}$. Ta inclui el conjunto del maga racional numeros con todo el maga entero numeros, que son maga fraccion con un denominador de 1. El simbolo del maga racional numero es $\mathbb {Q}$. Son el maga decimal fraccion como 0.3 and 25.12 un especial tipo de maga racional numero ya que el de ellos denominador es un potencia de 10. Por ejemplo, igual 0.3 a ${\tfrac {3}{10}}$, e igual 25.12 a ${\tfrac {2512}{100}}$. Ta corresponde cada racional numero a un finito o periodico decimal numero.

Tiene vez necesario el maga irracional numero para describi con maga magnitud na el geometria. Por ejemplo, irracional el longitud del hipotenusa de un rectangulo triangulo si ta tene el de suyo maga cateto con un longitud de 1.

El maga irracional numero son maga numero hinde expresable como el razon de dos maga entero. Maga ejemplo son manada cuadrao raiz, como ${\sqrt {2}}$, y maga numero como [[Pi|Plantilla:Pi]] y e (el numero de si Euler). Infinito, sin maga periodico decimal numero, el decimal representacion de un irracional numero. Ta constitui el conjunto del maga racional numero, junto con el conjunto del maga irracional numero, con el conjunto del maga real numero. El simbolo del maga real numero es $\mathbb {R}$. Ta inclui mas amplio maga clase de maga numero con el maga complejo numero y el maga cuaternion.

Basao na el uso del maga numero, clasificable como maga cardinal y maga ordinal numero. El maga cardinal numero —uno, dos, tres, etc.— son maga numero que ta expresa con el cantidad de maga objeto. Ta responde ellos al pregunta "¿cuanto?". Ta indica el maga ordinal numero —primero, segundo, tercero, etc.— con el orden o colocacion na un serie. Ta responde ellos al pregunta "¿cual posicion?".

Maga sistema de numeracion

Un cifra es un simbolo para representa con un numero, y maga sistema de numeracion son maga representacional marco. Usualmente ta tene ellos con un limitao cantidad de maga basico cifra, que directamente ta referi a cierto maga numero. Ta goberna el sistema paquemodo combinable este maga basico cifra para expresa con cualquier numero. El maga sistema de numeracion o posicional o hinde posicional. Todo el maga temprano sistema de numeracion hinde posicional. Na cuanto al maga hinde posicional sistema de numeracion, hinde ta depende el valor de un cifra del de suyo posicion na el numero.

El mas simple sistema hinde posicional es el unario sistema de numeracion. Ta confia ele na un simbolo lang, para el numero 1. Escrio todo el maga mas alto numero repitiendo con este simbolo. Por ejemplo, representable el numero 7 repitiendo siete maga vez con el simbolo para 1. Ta hace este sistema engorroso con el escritura de maga gran numero, razon por el cual ta inclui manada sistema hinde posicional con adicional maga simbolo para directamente representa con maga gran numero. Empleao maga variacion del unario sistema de numeracion na maga tallao palo, usando con maga abolladura, y na maga marca de conteo

Maga jeroglifico cifra desde 1 hasta 10,000

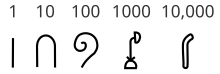
Ya conta el maga egipcio jeroglifico con un mas complejo hinde posicional sistema de numeracion, con adicional maga simbolo para tal maga numero como 10, 100, 1000 y 10,000. Combinable este maga numero na un suma para expresa mas convenientemente con maga mas grandes numero. Por ejemplo, ta usa el numero 10,405 con el simbolo para 10,000, cuatro maga vez el simbolo para 100, y cinco maga vez el simbolo para 1. Un similar bien conocio representacional marco es el romano sistema de numeracion, con el maga simbolo I, V, X, L, C, D, M como el de suyo maga basico cifra para representa con el maga numero 1, 5, 10, 50, 100, 500 y 1000.

Posicional un sistema de numeracion si na un compuesto expresion ta determina el posicion de un basico cifra con el de suyo valor. Ta tene el maga posicional sistema de numeracion con un base que ta actua como un multiplicando del maga diferente posicion. Para cada subsiguiente posicion, elevao el base a un superior potencia. Na el comun decimal sistema, tambien conocio como el indo-arabigo sistema de numeracion, 10 este base. Ta quere deci esto que el primer cifra multiplicao por $10^{0}$, el siguiente cifra multiplicao por $10^{1}$, y ansina sucesivamente. Por ejemplo, ta representa el decimal numero 532 con $5\cdot 10^{2}+3\cdot 10^{1}+2\cdot 10^{0}$. Gracias al efecto del maga posicion del maga cifra,, ta diferi el numero 532 del maga numero 325 and 253 masquen ta tene con el mismo maga cifra.

Otro posicional sistema de numeracion usao extensivamente na el computacional aritmetica es el binario sistema, que ta tene con un base de 2. Ta quere deci esto que el primer cifra multiplicao por $2^{0}$, el siguiente cifra multiplicao por $2^{1}$, y ansina sucesivamente. Por ejemplo, el numero 13 escrio como 1101 na el binario notacion, que ta representa con $1\cdot 2^{3}+1\cdot 2^{2}+0\cdot 2^{1}+1\cdot 2^{0}$. Na informatica, ta corresponde a un bit cada cifra del binario notacion. El mas temprano posicional sistema desarrollao por el maga babilonico y ya tene con un base de 60.

Maga aritmetico operacion

El maga aritmetico operacion son maga manera de combinar, transforma o manipula con maga numero. Son maga funcion que ta tene con maga numero como entrada y salida. El maga mas importante operacion na el aritmetica son el adicion, sustraccion, multiplicacion y division (matematica). Ta inclui maga adicional operacion con el potenciacion, el extraccion de maga raiz y el maga logaritmo. Si realizao este maga operacion na maga variable na cambio a maga numero, tiene vez denominao como maga algebraico operacion.

Dos maga importante concepto na relacion con el maga aritmetico operacion son el maga neutro elemento y el maga inverso elemento. Hinde ta causa elemento de identidad o elemento neutro de un operacion con ningun cambio si aplicao este a otro elemento. Por ejemplo, el neutro elemento de adicion es 0 ya que ta dale como resultao cualquier suma de un numero y 0 con el mismo numero. El elemento inverso es el elemento que ta dale como resultao con el elemento de identidad cuando combinao con otro elemento. Por ejemplo, el opuesto del numero 6 es -6 ya que el de ellos suma es 0.

Hay hinde lang maga inverso elemento sino maga inverso operacion. Na un informal acepcion, un operacion es el inverso de otro si ta deshace ele con el primer operacion. Por ejemplo, el sustraccion es el inverso del adicion ya que ta volve un numero al de suyo original valor si un segundo numero añadio y posteriormente sustraio, como na $13+4-4=13$. Mas formalmente definio, el operacion "$\star$" es un inverso del operacion "$\circ$" si ta cumpli con el siguiente condicion: $t\star s=r$ si y solo si $r\circ s=t$.

El conmutatividad y el asociatividad son maga ley gobernando con el orden na el que realizable algun maga aritmetico operacion. Conmutativo un operacion si cambiable el orden del maga argumento sin afecta con el maga resultao. Esto es el caso para el adicion, ya que por ejemplo $7+9$ el mismo como $9+7$. El asociatividad es un regla que ta afecta con el orden na el que realizable un serie de maga operacion. Asociativo un operacion si, na un serie de dos maga operacion, hinde ta importa el orden del maga operacion mismo. Esto es el caso para el multiplicacion, ya que por ejemplo $(5\times 4)\times 2$ el mismo como $5\times (4\times 2)$.

Adicion y sustraccion

El adicion es un aritmetico operacion na el que dos maga numeros, llamao el maga sumando, combinao na un solo numero, llamao el suma. El simbolo del adicion es $+$. Maga ejemplo $2+2=4$ y $6.3+1.26=7.56$. Usao el termino sumatorio si realizao manada adicion sucesivamente. El conteo es un tipo de repetio adicion na el que añadio el numero 1 sucesivamente.

El sustraccion es el inverso del adicion. Na ello, un numero, conocio como el sustraendo, removio de otro, conocio como el minuendo. El resultao de este operacion denominao el diferencia. El simbolo del sustraccion es $-$. Maga ejemplo $14-8=6$ and $45-1.7=43.3$. El sustraccion na manada situacion tratao como un especial caso del adicion: na cambio de sustrae con un positivo numero, tambien posible añadi con un negativo numero. Por ejemplo $14-8=14+(-8)$. Ta ayuda esto a simplifica con el maga matematico computacion reduciendo con el numero de maga basico aritmetico operacion necesario para realiza con maga calculo.

El aditivo neutro elemento de un elemento es 0 y el aditivo inverso de un numero es el negativo de aquel numero. Por ejemplo $13+0=13$ and $13+(-13)=0$. El adicion y conmutativo y asociativo.

Multiplicacion y division

El multiplicacion es un aritmetico operacion na el que dos maga numero, llamao el multiplicador y el multiplicando, combinao na un solo numero llamao el producto. El maga simbolo de multiplicacion son $\times$, $\cdot$, y *. Maga ejemplo $2\times 3=6$ y $0.3\cdot 5=1.5$. Si el multiplicando es un natural numero, entonces el multiplicacion es el mismo como el repetio adicion, como na $2\times 3=2+2+2$.

El division es el inverso del multiplicacion. Na ello, un numero, conocio como el dividendo, dividio na manada igual parte por otro numero, conocio como el divisor. El resultao de este operacion denominao el cociente. El maga simbolo de division son $\div$ y $/$. Maga ejemplo $48\div 8=6$ y $29.4/1.4=21$. El division na manada situacion tratao como un especial caso del multiplicacion: na cambio de dividi con un numero, tambien posible por el de suyo reciproco. El reciproco de un numero es 1 dividio por aquel numero. Por ejemplo $48\div 8=48\times {\tfrac {1}{8}}$.

El multiplicativo identidad es 1 y el multiplicativo inverso de un numero es el reciproco de aquel numero. Por ejemplo $13\times 1=13$ y $13\times {\tfrac {1}{13}}=1$.El multiplicacion y conmutativo y asociativo.

Potenciacion y logaritmo

El potentiacion es un aritmetico operacion na el que un numero, conocio como el base, elevao al potencia de otro numero, conocio como el exponente. El resultao de este operacion denominao el potencia. Tiene vez expresao el potenciacion usando con el simbolo ^ pero el mas comun modo es escribi con el exponente na superindice justo despues del base. Maga ejemplo $2^{4}=16$ and $3$^$3=27$. Si el exponente es un natural numero, entonces el potenciacion es el mismo como el repetio multiplicacion, como na $2^{4}=2\times 2\times 2\times 2$.

Son el maga raiz un especial tipo de multiplicacion usando con un fraccional exponente. Por ejemplo, el cuadrao raiz de un numero es el mismo como elevando con aquel numero al potencia de ${\tfrac {1}{2}}$ y el cubico raiz de un numero es el mismo como elevando con aquel numero al potencia de ${\tfrac {1}{3}}$ Maga ejemplo ${\sqrt {4}}=4^{\frac {1}{2}}=2$ y ${\sqrt[{3}]{27}}=27^{\frac {1}{3}}=3$.

El logaritmo es el inverso del potenciacion. El logaritmo de un numero $x$ al base $b$ es el exponente al que hay que eleva con $b$ para produci con $x$. Por ejemplo, ya que $1000=10^{3}$, el logaritmo na base 10 de 1000 es 3. El logaritmo de $x$ na base $b$ denotao como $\log _{b}(x)$, o sin maga parentesis, $\log _{b}x$, o hasta sin el explicito base, $\log x$, cuando entendible el base por el contexto. Ansina, expresable el anterior expresion como $\log _{10}1000=3$.

Hinde ta tene el potenciacion y el logaritmo con maga general neutro elemento y maga inverso elemento como el adicion y el multiplicacion. El neutro elemento del potenciacion na relacion al exponente es 1, como na $14^{1}=14$. Sin embargo, hinde ta tene el potenciacion con un general neutro elemento ya que 1 hinde el neutro elemento para el base. El potenciacion y el logaritmo ni conmutativo ni asociativo.

Maga tipo de aritmetica

Na el academico literatura discutio maga diferente tipo de maga aritmetico sistema .El maga diferencia basao na el tipo de numero considerao, el sistema de numeracion empleao, y si ta opera ellos na maga matematico objeto que hinde maga numero.

Aritmetica de maga entero

El aritmetica de maga entero es el rama de aritmetica que ta trata con el manipulacion de maga positivo y negativo entero. Maga operacion de un solo cifra realizable siguiendo o memorizando con un tabla que ta presenta con el maga resultao de todo el maga posible combinacion, como un tabla de adicion o un tabla de multiplicacion. Otro maga comun metodo son el verbal conteo y conta con el maga dedo.

Tabla de adicion

+	0	1	2	3	4	...
0	0	1	2	3	4	...
1	1	2	3	4	5	...
2	2	3	4	5	6	...
3	3	4	5	6	7	...
4	4	5	6	7	8	...
...	...	...	...	...	...	...

Tabla de Multiplicacion

×	0	1	2	3	4	...
0	0	0	0	0	0	...
1	0	1	2	3	4	...
2	0	2	4	6	8	...
3	0	3	6	9	12	...
4	0	4	8	12	16	...
...	...	...	...	...	...	...

Ejemplo de adicion con acarreo. El maga negro numero son el sumando, el verde numero es el acarreo y el azul numero es el suma.

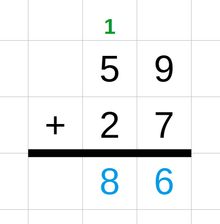
Para maga operacion con maga numero con mas de un cifra, usable diferente maga tecnica para calcula con el resultao usando manada operacion de un solo cifra sucesivamente. Por ejemplo, na el metodo de adicion con acarreo, el dos maga nmeros escrio uno encima del otro. Empezando con el cifra mas al derecha, sumao cada par de maga cifra. El cifra mas al derecha del suma escrio debajo de ellos. Si el suma es un numero de dos maga cifra, entonces el cifra al izquierda, llamao el "acarreo", añadio al siguiente par de maga cifra al izquierda. Repetio este proceso hasta que añadio todo el maga cifra. Otro maga metodo usao para el adicion de maga entero son el metodo del real recta, el metodo de maga parcial suma y el metodo de compensacion. Utilizao un similar tecnica para el sustraccion: tambien ta empeza ele con el cifra mas al derecha y ta utiliza con un "prestamo" o un negativo acarreo para el columna al izquierda si negativo el resultao del sustraccion de un solo cifra.

Ejemplo de largo multiplicacion. El maga negro numero son el multiplicador y el multiplicando. El maga verde numero son el maga intermediario producto ganao multiplicando con el multiplicador con un solo cifra del multiplicando. El azul numero es el total producto calculao añadio con el maga intermediario producto.

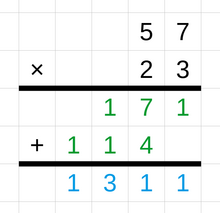
Ta emplea un basico tecnica del multiplicacion de maga entero con el repetio adicion. Por ejemplo, el producto de 3 × 4 calculable como 3 + 3 + 3 + 3. Un comun tecnica para el multiplicacion con maga gran numero es el largo multiplicacion. Ta empeza este metodo escribiendo con el multiplicador encima del multiplicando. Ta empeza el calculo multiplicando con el multiplicador solo con el cifra mas al derecha del multiplicando y escribiendo con el resultado a continuacion, empezando na el columna mas al derecha. Ta ocurri el mismo para cada cifra del multiplicando, y na cada caso, ta muda el resultao por un posicion al izquierda. Como final paso, sumao todo el maga individual producto para llega al total producto del dos maga numero de vario maga cifra.. Otro maga tecnica usao para el multiplicacion son el metodo del cuadricula y el multiplicacion de celosia. Interesao el informatica na el maga algoritmo de multiplicacion con un bajo complejidad de computacion para multiplica eficientemente con maga muy grande entero, como el algoritmo de si Karatsuba, el Algoritmo de si Schönhage-Strassen y el algoritmo de si Toom-Cook. Un comun tecnica usao para el division denominao el largo division. Ta inclui otro maga metodo con el corto division y el fragmentacion.

El aritmetica de maga entero hinde cerrao bajo el division. Ta significa esto que al dividi con un entero por otro, el resultao hinde firmi un entero. Por ejemplo, 7 dividio por 2 hinde un entero sino 3.5. Un metodo para asegura que el resultao es un entero es redondea con el resultao a un entero. Sin embargo, ta conduci este metodo a maga imprecision porque alterao el original valor. Otro metodo es realiza con el division, pero parcialmente lang, y retene con el resto. Por ejemplo, 7 dividio por 2 es 3 con un resto de 1. Ta evita este maga dificultad el aritmetica de maga racional numero, que ta permiti con el exacto representacion de maga fraccion.

Un simple metodo para calcula con el potenciacion es el repetio multiplicacion. Por ejemplo, el potenciacion de 3⁴ calculable como 3 × 3 × 3 × 3. Un mas eficiente tecnica usao para maga gran exponente es el binario exponenciacion. Ta fragmenta ele con el calculacion na manada operacion de cuadra. Por ejemplo, el potenciacion 3⁶⁵ expresable como (((((3²)²)²)²)²)² × 3. Utilizando con maga repetido operacion de cuadra, solo 7 maga individual operacion necesario imbes del 64 maga operacion necesario para el regular repetio multiplicacion. Para calcula con el maga logaritmo, ta inclui maga metodo con el maga serie de si Taylor y el maga continuo fraccion. El aritmetica de maga entero hinde cerrao, ni bajo el logaritmo ni bajo el potenciacion con maga negativo exponente, que ta significa que hinde firmi un entero el resultao de este maga operacion.

Teoria de maga numero

Ta estudia el teoria de maga numero con el estructura y el maga propiedad del maga entero ademas del mag relacion y maga ley entre ellos. Ta inclui cuanto maga principal rama del teoria de maga numero con el elemental teoria de maga numero, el analitico teoria de maga numero, el teoria de maga algebraico numero y el geometria de maga numero. Ta estudia el elemental teoria de maga numero con el maga aspecto del maga numero investigable por maga elemental metodo. Na este acepcion, excluio el uso de maga metodos incuntao na el analisis y el calculo. Ta inclui el de suyo maga tema con el divisibilidad, el factorizacion y el primalidad. El analitico teoria de maga numero, por el contrario, basas na maga tecnicas de analisis y calculo. Ta examina ele con tal maga problema como el distribucion del maga primo numero y el afirmacion de que todo par nnmero es un suma de dos maga primo numero. Ta emplea el teoria de maga algebraico numero con maga algebraico estructura para analiza con el maga propiedad de, y maga relacion entre, el maga numero. Maga ejemplo el uso de maga cuerpo y maga anillo, como na tal maga cuerpo de maga algebraico numero como el anillo de maga entero. Ta usa el geometria de maga numero con maga concepto del geometria para estudia con el maga numero. Por ejemplo, ta investiga ele con el comportamiento de maga red, con maga entero coordenada, na un plano. Adicional maga rama del teoria de maga numero son el probabilistico teoria de maga numero, el combinatorio aritmetica, el computacional teoria de maga numero y el aplicao teoria de maga numero.

Na el teoria de maga numero, ta inclui maga influyente teorema con el fundamental teorema del aritmetica, el teorema de si Euclides y el ultimo teorema de si Fermat. Segun el fundamental teorema del aritmetica, cada entero mayor que 1 es (1) un primo numero o (2) representable como un distinto producto de maga primo numero. Por ejemplo, el numero dieciocho hinde un primo numero y representable como $2\times 3\times 3$, todo del que son maga primo numero. El numero diecinueve, por el contrario, es un primo numero, ansina que hinde ta tene con otro primo factorizacion. Ta afirma el teorema de si Euclides que hay maga infinito primo numero. El ultimo teorema de si Fermat es el afirmacion de que nuay ningun maga positivo entero $a$, $b$ y $c$ que ta soluciona con el ecuacion $a^{n}+b^{n}=c^{n}$ si $n$ mayor que $2$.

Aritmetica de maga racional numero

El aritmetica de maga racional numero es el rama del aritmetica que ta trata con el manipulacion de maga numero expresable como un razon de dos maga entero. Na cuanto al mayoria del maga aritmetico operacion na el maga racional numero, calculable realizando con un serie de maga entero aritmetico operacion na el mage numerador y el maga denominador del maga numero involucrao. Si ta tene dos maga racional numero con el mismo denominador, posible añadi con ambo maga, añadiendo con el maga numerador y reteniendo con el comun denominador. Por ejemplo, ${\tfrac {2}{7}}+{\tfrac {3}{7}}={\tfrac {5}{7}}$. Ta existi un similar procedimiento para el sustraccion. Si hinde ta tene el dos maga numero con el mismo denominador, primero hay que transforma con ellos para incuntra con un comun denominador. Realizable esto escalando con el primer numero por el denominador del segundo numero mientras escalando con el segundo numero por el denominador del primer numero. Por ejemplo, ${\tfrac {1}{3}}+{\tfrac {1}{2}}={\tfrac {1\cdot 2}{3\cdot 2}}+{\tfrac {1\cdot 3}{2\cdot 3}}={\tfrac {2}{6}}+{\tfrac {3}{6}}={\tfrac {5}{6}}$.

Dos maga racional numero multiplicao multiplicando con el de ellos maga numerador y el de ellos maga denominador respectivamente, como na ${\tfrac {2}{3}}\cdot {\tfrac {2}{5}}={\tfrac {2\cdot 2}{3\cdot 5}}={\tfrac {4}{15}}$. Realizable el division de un racional numero por otro, multiplicando con el primer numero por el [[reciproco[[ del segundo numero. Ta significa esto que ta cambia de posicion el numerador y el denominador del segundo numero. Por ejemplo, ${\tfrac {3}{5}}:{\tfrac {2}{7}}={\tfrac {3}{5}}\cdot {\tfrac {7}{2}}={\tfrac {21}{10}}$. Hinde como el aritmetica de maga entero, el aritmetica de maga racional numero cerrao bajo el division, con tal de que el divisor hinde 0.

Ni el aritmetica de maga entero, ni el aritmetica de maga racional numero, cerrao bajo el potenciacion o el logaritmo. Un manera de calcula con el exponenciacion con un fraccional exponente es un serie de dos maga calculo: (1) un potenciacion usando con el numerador del exponente, seguio por (2) el extraccion del enesimo raiz del resultao basao na el denominador del exponente. Por ejemplo, $5^{\frac {2}{3}}={\sqrt[{3}]{5^{2}}}$. Realizable el primer operacion por tal maga metodo como el repetio multiplicacion, o el potenciacion por cuadra. Un manera, para obtene con un aproximao resultao para el segundo operacion, es el uso del metodo de si Newton, que ta usa con un serie de maga etapa para gradualmente refina con un inicial conjetura hasta que ta alcanza al deseao nivel de precision. Para calcula con maga logaritmo, utilizable maga serie de si Taylor, o el metodo de maga continuo fraccion.

El notacion de un decimal fraccion es un especial manera de representa con maga que representan números racionales cuyo denominador es una potencia de 10 numero cuyo denominador es un potencia de 10. Por ejemplo, el maga racional numero ${\tfrac {1}{10}}$, ${\tfrac {371}{100}}$ y ${\tfrac {44}{10000}}$ escrio como 0.1, 3.71 y 0.0044 bajo el decimal sistema de numeracion. Para maga calculo con maga decimal fraccion, aplicable maga modificao version de maga metodo para el calculo con maga entero, como el adicion con acarreo, y el largo multiplicacion. Hinde ta tene todo el maga racional numero con un finito representacion na el decimal notacion. Por ejemplo, ta corresponde el racional numero ${\tfrac {1}{3}}$ a 0.333... con infinito maga 3. El abreviao notacion para este tipo de periodico decimal numero es 0.Plantilla:Overline. Ta expresa cada periodico decimal con un racional numero.

Aritmetica de maga real numero

El aritmetica de maga real numero es el rama del aritmetica que ta trata con el manipulacion del maga numero, o racional o irracional. El maga irracional numero son el maga numero inexpresable por maga fraccion o maga periodico decimal, como el cuadao raiz de 2, y el numero π. Hinde como el aritmetica de maga racional numero, el aritmetica de maga real numero cerrao bajo el potenciacion, con tal de que el base es un positivo numero. Verdadero el mismo para el logaritmo de maga positivo real numero, con tal de que el base del logaritmo es positivo y mayor que 1.

Ta involucra el maga irracional numero con un infinito serie de maga decimal cifra que hinde ta repeti. Debio a esto, na manada situacion nuay ningun sencillo y preciso metodo para expresa con el maga resultao de tal maga aritmetico operacion como ${\sqrt {2}}+\pi$ or $e\cdot {\sqrt {3}}$. Si hinde necesario absoluto precision, tipicamente ta basta el truncamiento o el redondeo para trata con el problema del calculo de maga aritmetico operacion na maga real numero. Ta retene el truncamiento con un cierto numero de maga significante cifra al izquierda, y ta remove con el maga adicional cifra al derecha del ultimo significante cifra. Por ejemplo, ta tene el numero π con un infinito cantidad de maga cifra empezando por 3.14159... . Si ta necesita kita con cuatro maga significante cifra gayot, el resultao 3.141. El redondeo es un similar proceso na el que ta aumenta el ultimo significante cifra es 5 o mayor. Si el siguiente cifra es mayor que 5, ta queda el mismo el ultimo cifra. Por ejemplo, si ta redondea con el numero π a cuatro maga significante cifra, el resultao 3.142 porque el siguiente cifra es 5. Esencial este maga metodo para permiti con el maga calculo na el maga real numero por maga computadora.

Na manada situacion, ta expresa el normalizao cientifico notacion con maga numero muy grande o muy chico. Na este notacion, ta representa este maga numero un llamao significando multiplicao por un potencia de 10. El significando es un cifra seguio por un decimal punto y un serie de maga cifra. Por ejemplo, el normalizao cientifico notacion del numero 8276000 es $8.276\times 10^{6}$, mientras que el del numero 0.00735 es $7.35\times 10^{-3}$.

El aritmetica na flotante coma es un comun metodo empleao por el maga computadora para aproxima con el aritmetica de maga real numero. Ta representa ele con el maga real numero por un metodo similar al del cientifico notacion por medio de tres maga numero: un significando, un base y un exponente. Limitao el precision del significando por el numero de maga bit alocao para representa conele. Si ta dale como resultado un aritmetico operacion con un numero que ta requeri con mas maga bit que disponible, ta redondea el computadora con el resultao al mas cercano representable numero. Ta conduci esto a maga error de redondeo. Un consecuencia de este comportamiento es que ta viola el aritmetica na flotante coma con maga cierto ley del aritmetica. Por ejemplo, hinde asociativo el aritmetico na flotante coma, ya que na cuanto al maga error de redondeo, baka ta depende ellos na el orden del maga adicion. Ta significa esto que el resultao de $(a+b)+c$ tiene vez diferente del resultao de $a+(b+c)$. El mas comun tecnico estandar usao para el aritmetica na flotante coma es IEEE 754. Entre otro maga cosa, ta determina ele con el representacion de maga numero, el estandara para el maga aritmetico operacion y el redondeo, y el manejo de maga error y maga excepcion. Si el velocidad de computacion hinde un limitando factor, posible el aritmetico de arbitrario precision, para el que ta restringi el memoria lang del computadora con el precision de maga calculo.

Otro maga

Ejemplo de modular aritmetica usando con un reloj: despues de añadi con 4 maga hora al maga 9 na punto, de nuevo ta empeza al inicio el manecilla y ta apunta al 1 na punto.

Hay manada otro tipo del aritmetica. Ta opera el modular aritmetica na un finito conjunto de maga numero. Si ta conduci un operacion a un numero fuera de este finito conjunto, entonces ajustao de nuevo el numero na el conjunto, de similar manera a como ta comenza el maga manecillas del maga reloj al principio de nuevo despues de completa con un ciclo. El modulo es el numero al que ta pasa este ajuste. Por ejemplo, ta tene un regular reloj con un modulo de 12. Na cuanto al adicion de 4 a 9, ta significa esto que el resultao hinde 13 sino 1. Aplicable este principio a otro maga operacion, como el sustraccion, el multiplicacion y el division.

Ta trata algun maga forma de aritmetica con maga operacion realizao na maga matematico objeto hinde numerico. Ta describi el aritmetica de maga intervalo con maga operacion na maga intervalo. Usable este maga intervalo para representa con un rango de maga valor, si desconocio el preciso magnitud, por ejemplo, debio a maga error de medicion. Ta inclui el aritmetica con tal operacion como el adicion y el multiplicacion na maga intervalo, como na $[1,2]+[3,4]=[4,6]$ y $[1,2]\times [3,4]=[3,8]$. Estrechamente relacionao esto al afin aritmetica, cuyo meta es maga mas preciso resultao realizando con maga calculo na maga afin forma imbes de maga intervalo. Un afin forma es un numero junto con maga termino de error que ta describi el posible desviacion del numero al verdadero magnitud. Ta describi el aritmetica de maga vector y el aritmetica de maga matriz con maga aritmetico operacion na maga vector y maga matriz, como el adicion de maga vector y el multiplicacion de maga matriz.

Realizao el mental calculo exclusivamente na el mente sin depende de maga externo ayuda.

Para el mental calculo, el maga calculo realizao exclusivamente na el mente sin herramientas externas como lapiz y papel o maga electronico calculadora. Na cambio, ta utiliza el mental calculo con el visualizacion, el memorizacion y cierto maga tecnica de calculacion para soluciona con maga aritmetico problema. Uno de aquel maga tecnicas es el metodo de compensacion. Ta consisti na el alteracion del maga numero para facilita con el calculo, y mas tarde ajustando con el resultao. Por ejemplo, imbes de $85-47$, mas facil el calculo de $85-50$ porque ta involucra conele un redondo numero. Na el siguiente paso, añadio 3 al resultao para compensa con el anterior ajuste. Frecuentemente ensañao el mental calculo na el primario educacion para entrena con el maga numerico habilidad del maga estudiante.

Clasificable el maga sistema de aritmetica basao na el sistema de numeracion empleao, por ejemplo el decimal sistema de numeracion). Otro maga ejemplo son el binario sistema, el octal sistema y el hexadecimal sistema.

Ta describi el aritmetica de maga compuesto unidad con el maga aritmetico operacion realizao na maga magnitud con maga compuesto unidad. Ta involucra ele con maga adicional operacion para goberna con el transformacion entre maga cantidad de un solo unidad y ellos de un compuesto unidad. Por ejemplo, usao el operacion de reduccion para transforma con el compuesto cantidad de 1 h 90 min al simple cantidad de 150 min.

El maga hinde diofantico aritmetica son maga sistema de aritmetica que ta viola con maga tradicional aritmetico intuicion y ta inclui con tal maga ecuacion como $1+1=1$ and $2+2=5$. Empleable allos para representa con algun maga situacion (del real mundo), y na el moderno fisica y na el cotidiano vida. Por ejemplo, usable el ecuacion $1+1=1$ para describi con el observacion de que, si agregao un gota de ulan a otro gota de ulan, entonces hinde ta permanece ellos como dos maga distinto entidad, sino que ta queda uno.

Maga axiomatico fundacion

Ta trata el maga axiomatico fundacion del aritmetica de proporciona con un chico conjunto de maga ley, llamao maga axioma, del que derivable todo el maga fundamental propiedad del maga numero y el maga operacion sobre ellos. Ta constitui ellos con maga representacional marco, logicamente coherente y sistematico, usable al de suyo vez para formula con maga matematico demostracion con rigor. Dos maga bien conocio marco son el maga axioma de si Peano y el maga construccion del teoria de maga conjunto.

Ta proporciona el maga axioma de si Peano con un axiomatizacion del aritmetica del maga natural numero. El de ellos maga basico principio primero formulao por si Richard Dedekind y mas tarde refinao por si Giuseppe Peano. Basao ellos lang na un chico numero de maga primitivo matematico concepto, como 0, el maga natural numero y un sucesor. Ta determina el maga axioma de si Peano con el relacion de este maga concepto. Todos el demas maga aritmetico concepto definible na mage términos de este maga primitivo concepto.

1. 0 un natural numero.
2. Para cada natural numero, hay un sucesor, tambien un natural numero.
3. Nunca identico el maga sucesor de dos maga diferente natural numero.
4. 0 hinde el sucesor de un natural numero.
5. Si ta contene un conjunto con 0 y cada sucesor entonces ta contene con cada natural numero.

Ta expresa el repetio aplicacion del funcion sucesor $s$ con el maga numero mayor que 0. Por ejemplo, $1$ es $s(0)$ y $3$ es $s(s(s(0)))$. Definible el maga aritmetico operacion como maga mecanismo que ta afecta con el aplicacion del funcion sucesor. Por ejemplo, añadi con $2$ es el mismo que aplica con el funcion sucesro a este numero.

Ta utiliza manada axiomatizacion del aritmetica con el teoria de maga conjunto. Ta cubri ellos con el maga natural numero, pero tambien extensible al maga entero, el maga racional numero, y el real numero. Representao cada natural numero por un distinto conjunto. 0 usualmente definio por el vacio conjunto $\varnothing$. Cada subsiguiente numero definible como el union del anterior numero con el conjunto conteniendo con el anterior numero. Por ejemplo, $1=0\cup \{0\}=\{0\}$, $2=1\cup \{1\}=\{0,1\}$, y $3=2\cup \{2\}=\{0,1,2\}$. El maga entero definible como maga ordenao par de maga natural numero donde el segundo numero sustraio del primero. Por ejemplo, ta representa el par (9, 0) con el numero 9 mientras que ta representa el par (0, 9) con el numero -9. El maga racional numero definible como maga par de maga entero donde ta representa el primer numero con el numerador y ta representa el segundo con el denominador. Por ejemplo, ta representa el par (3, 7) con el racional numero ${\tfrac {3}{7}}$. Para construi con el maga real numero, ta usa un metodo con el concepto de maga corte de s Dedekind. Segun este enfoque, ta representa cada real numero un particion de todo el maga racional numero na dos maga conjunto, uno para todo el maga numero mas abajo del representao real numero y el otro para el demas. El maga aritmetico operacion definio como maga funcion que ta realiza con vario transformacion (del teoria de maga conjunto) na el maga conjunto representando con el maga numero de entrada, para produci con el conjunto representando con el resultao (o salida).

Ta interpreta algun maga historiador con el hueso de Ishango como uno del maga primero aritmetico artefacto.

El conteo y el maga marca de conteo, usao para llevar con un registro del maga cantidad, tiene vez considerao como el maga mas temprano forma del aritmetica. Ta sugeri algun maga historiador que el hueso de Lebombo (hace alrededor de 43,000 maga año) y el hueso de Ishango (hace alrededor de 22,000–30,000 maga año) son el mas antiguo aritmetico artefacto, pero disputao este interpretacion. Sin embargo, puede antedata un basico numerico sentido con este maga artefacto, y baka hasta el desarrollo del lenguaje.

Hinde hasta del surgimiento de maga antiguo civilizacion que ya comenza a evoluciona, a partir del año 3000 AEC, un mas complejo y estructurao enfoque al aritmetica. Necesario este desarrollo gracias al aumentao necesidad de anota con el maga almacenao articulo, administra con el propiedad del tierra y organiza con maga intercambio. Ya desarrolla todo el maga principal antiguo civilizacion con maga hinde posicional sistema de numeracion para facilita con el representacion de maga numero. Ademas ya tene ellos con maga simbolo para tal operacion como el adicion y el sustraccion, y ya conoce ellos con maga fraccion. Maga ejemplo el maga egipcio jeroglifico ademas del maga sistema de numeracion inventao na Sumeria, China e India. Ta desarrolla el maga babilonico con el primer posicional notacion a partir del año 1800 AEC. Esto un significante mejora con respecto al maga anterior sistema de numeracion, ya que ya hace mas eficiente con el representacion de maga grandes numeros y el maga calculos sobre ellos. Desde la antigüedad, utilizao tambien maga abaco como maga manual herramienta de calculo, como eficiente medio para realiza con maga complejo calculo.

Utilizao el maga abaco como manual herramienta de calculo na maga antiguo civilizacion, como el Suanpan na China.

Primariamente ta usa el maga temprano civilizacion con el maga numero para maga concreto practico proposito y ta carece ellos de un abstracto concepto del numero mismo. Ya cambia esto con el griego matematica, que ya inicia con un exploracion del abstracto naturaleza del maga numero, hinde lang el estudio del aplicacion de maga numero a maga especifico problema. Otro novedoso característica el uso de maga prueba para establece con maga matematico verdades y valida con maga teorias. Otro contribucion el de ellos distincion de manada clase de maga numero, como el maga par e impar numero, y el maga primo numero. Ya inclui esto con el descubrimiento de que el maga numeros para maga cierto geometrico longitud son irracional y, por lo tanto, inexpresable como maga fraccion. Considerao como el incepcion del griego matematica el maga obra de si Tales de Mileto y de si Pitagoras na el aca-7 y aca-6 siglo AEC. Si Diofanto de Alejandria un influyente figura na el griego aritmetica, na el aca-3 siglo AEC, por el de suyo numeroso contribucion al teoria de maga conjunto y el de suyo exploracion del aplicacion de maga aritmetico operacion a maga algebraico ecuacion.

El maga antiguo indio el maga primero na desarrolla con el concepto de cero como un numero usable na maga calculo. Alrededor de 628 EC, ya escribi si Brahmagupta con el maga exacto regla del funcionamiento de cero. Ya existi ya el concepto de cero o nada, pero hinde considerao como un matematico objeto, apto para el maga aritmetico operacion. Ademas ya provee si Brahmagupta con un detallao discusion del maga calculo con maga negativo número, y el de ellos aplicacion a tal maga problema como el credito y el deuda. Significativamente mas antiguo el concepto del maga negativo numero mismo, y primero explorao na el chino matematica durante el primer milenio AEC.

Ademas ya desarrolla el maga indio matematico con el indo-arabigo numeracion usao hoy, particularmente el concepto de un cifra para cero na lugar de maga vacio o faltante posicion. Por ejemplo, ya provee si Aryabhata con un detallao tratamiento del de suyo maga operacion alrededor del maga principio del aca-6 siglo EC. Ya sufri el indio decimal sistema con mas refinamiento, incluio un expansion al maga hinde entero, durante el Edad de Oro del islam por tal arabe matematico como si Al-Juarismi. Ta introduci el de suyo influyente obra con el decimal sistema de numeracion al occidente, que na aquel entonces ya usa pa con el romano numeracion. Aqui, ya populariza esto tal maga matematico como si Leonardo de Pisa, que ya vivi durante el aca-13 y aca-12 siglo y ademas ya desarrolla con el sucesion de si Fibonacci. Durante el Medio Edad y el Renacimiento, publicao manada popular libro de texto para facilita con el maga practico calculo para el comercio. Durante este periodo ya generaliza el uso de maga abaco. Durante el aca-16 siglo, ya concebi el matematico si Gerolamo Cardano con el concepto del maga complejo numero como un metodo de soluciona con el maga ecuacion de tercer grado.

El stepped reckoner de si Leibniz fue el primer calculadora capaz de realiza con todo el cuatro maga aritmetico operacion.

Durante el aca-18 y aca-19 siglo, ya senta tal maga matematico como si Leonhard Euler y si Carl Friedrich Gauss con el maga base para el moderno teoria de maga numero. Otro desarrollo durante este periodo fue el trabajo sobre el formalizacion y el maga fundamento del aritmetica, como el teoria de maga conjunto de si Georg Cantor y el maga axioma de si Peano usao como un axiomatizacion del aritmetica de maga natural numero. Durante el aca -20 siglo desarrollao el maga computadora y el maga calculadora. Ya revolucioniza el de ellos amplio uso con el precision y velocidad por el que calculable cada vez mas complejo aritmetico computo.

Na manada campo

Educacion

El aritmetico educacion es parte del primario educacion. Es uno del primer maga forma de matematico educacion que ta incuntra el maga niño. El meta del elemental aritmetica es el entrega, al maga estudiante, de un basico numerico sentido, y un familiaridad con el maga fundamental numerico operacion como el adicion, el sustraccion, el multiplicacion y el division. Na manada situacion introducio na relacion con maga concreto escenario, como conta con maga abalorio, dividi con el clase na maga grupo de maga niño del mismo tamaño, y el computo de cambio al realiza con maga compra. Maga comun herramienta na el temprano aritmetico educacion son maga real recta, maga tabla de adicion y multiplicacion, y maga bloque de base diez.

Ta enfoca maga posterior etapa na un mas abstracto entendimiento. Ta introduci ellos al maga estudiante con maga diferente tipo de maga numeros, como negativo numero, maga fraccion, maga real numero y maga complejo numero. Ademas ta cubri ellos con mas avanzao numerico operacion, como el potenciacion, el extraccion de maga raiz y el logaritmo. Tambien ta mostra ellos con el empleo del maga aritmetico operacion na otro maga rama del matematica, como el de ellos eplicacion para describi con el maga geometrico forma y el uso del maga variable na el algebra. Otro aspecto es el enseñanaza, al maga estudiante, de maga algoritmo y maga calculadora para soluciona con maga complejo aritmetico problema.

Psicologia

Interesao el psicologia del aritmetica na el aprendizaje, y por maga humano y por maga animal, ademas del representacion del maga numero y el de ellos empleo para maga calculo. Ta examina ele con el entendimiento y solucion de maga matematico problema, ademas del relacion entre el maga aritmetico habilidad y otro maga cognitivo caracteristica, como el percepcion, el memoria, el juicio y el toma de maga decision. Por ejemplo, ta investiga ele con el primer encuentro de maga coleccion de maga concreto articulo na el percepcion, y el de ellos subsiguiente asociacion con maga numero. Ta trata otro campo de investigacion con el relacion entre el maga numerico calculo y el uso del lenguaje para forma con maga representacion. Tambien ta expora el psicologia con el biologico origen del aritmetica como innato capacidad. Ta referi esto a maga pre-verbal y pre-simbolico cognitivo proceso, implementando con maga aritmetico operacion necesario para exitosamente representa con el mundo y realiza con tal maga tarea como el espacial navegacion.

Uno del maga concepto estudiao por el psicologia es el numerismo, o el capabilidad de comprende con maga numerico concepto, aplica con ellos a maga concreto, situacion y razona con ellos. Ta inclui ele con un fundamental numerico sentido ademas del habilidad para estima y compara con maga cantidad. Ademas ta abarca ele con el maga habilidades para representa simbolicamente con el maga numeros na maga sistema de numeracion, interpretar con maga maga numerico dato y evalua aritmetico calculo. El numerismo un clave habilidad na manada academico campo. Puede un falta de numerismo inhibi con academico exito y conduci a maga mal economico decision na el cotidiano vida, por ejemplo, al malinterpreta con el maga plan de maga hipotecario y el maga poliza de seguro.

Filosofia

Ta estudia el filosofia del aritmetica con el maga fundamental concepto y principio que ta subyace con el maga numero y el maga aritmetico operacion. Ta explora ele con el naturaleza y ontologico estado del maga numero, el relacion del aritmetica con el lenguaje y el logica. y el adquisicion del aritmetico conocimiento.

Segun el platonismo, ta disfruta el maga numero de un existencia independiente del mente: ta existi como maga abstracto objeto, fuera del espacio-tiempo y sin maga causal poder. Ta rechaza este punto de vista el intuicionismo, que ta afirma que el maga matematico objeto son maga mental construccion. Otro maga teoria son el logicismo, que ta afirma que reducible maga matematico verdad a maga logico verdad, y el matematico formalismo, que ta afirma que el maga matematico principio son maga regla para el manipulacion de maga simbolo, sin declara que ta corresponde ellos a maga entidad fuera de este actividad gobernao por maga regla.

El punto de vista tradicionalmente dominante na el epistemologia del aritmetica es que el maga aritmetico verdad cognoscible a priori. Ta significa esto que cognoscible ellos por el pensamiento lang, sin necesidad de confia na el maga dato del maga sentido de antemano. Ta afirma algun maga proponente de este punto de vista que innato el aritmetico conocimiento, mientras que ta declara otro maga que hay algun forma de logico intuicion por el que comprensible el maga matematico verdad. Mas recientemente ta sugeri tal maga naturalista como si Willard Van Orman Quine con un alternativo punto de vista: que el maga matematico principio son maga generalizacion de alto nivel al final arraigao na el sensorial mundo descrio por el maga empirico ciencia.

Otro maga

Relevante el aritmetica a manada campo. Na el cotidiano vida, necesario para calcula con el cambio al realiza con maga compra, para maneja con el maga personal finanza, y ajusta con un receta de cocina para un diferente numero de maga porcion. Ta emplea el maga negocio con el aritmetica para calcula con el maga ganancias y maga perdida y analiza con el maga tendencia de mercado. Na el campo del ingenieria, usao para medi con maga cantidad, calcula con maga carga y maga fuerza, y diseña con maga estructura. Ta confia el criptograifa na el maga aritmetico operacion para protege con sensitivo informacion por el cifrao para codifica con el maga dato y el maga mensaje.

Ta yace el maga aritmetico operacion al fundacion de manada rama del matematica, como el algebra, el calculo y el estadistica. Por medio de ellos, ta extende el influencia del aritmetica al mayoria del maga ciencia, como el fisica, el maga ciencia del computacion y el Economia. Usao este maga operacion na el maga calculo, el resolucion de maga problema, el analisis de maga dato y el maga algoritmo, ansina que integral ellos al cientifico investigacion, el tecnologico desarrollo y el economico modelacion.

Mira tambien

• Portal:Ciencia y Matematico. Contenido relacionado con Ciencia y Matematico.
• Algorismo
• Aritmetica de finito cuerpo
• Resumen del aritmetica